卡尔曼滤波

　　卡尔曼滤波对机器人研究来说是一个比较常用的方法，这篇博客主要根据CS373: Artificial Intelligence for Robotics这门公开课的内容做简要的介绍。

高斯分布

　　高斯分布是一个连续的单峰图像（continuous, uni-model)，如下图所示，表示的是一个概率分布。高斯分布可以通过均值μ和方差σ^2来共同确定它的位置和形状。当x=μ时，f(x)有最大值；σ^2越大，图像越矮胖，不确定性越大，反之亦然。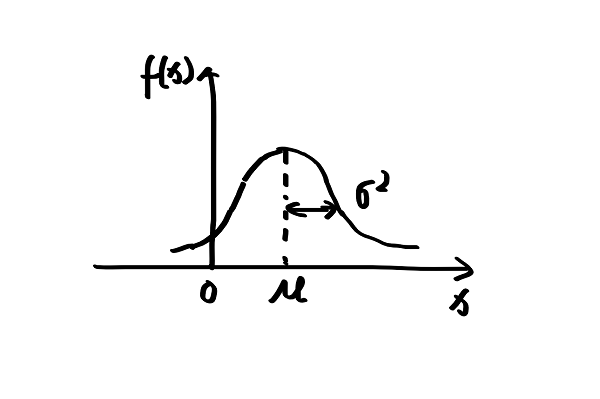

　　用数学公式描述如下：
$$ f(x) = \frac{1}{\sqrt{2πσ^2}} exp^{-\frac12 \frac{(x-μ)^2}{σ^2}} $$

$$ \int_{-\infty}^\infty f(x)dx = 1 $$

Measure Gaussian

　　在prior Gaussian的基础上，我们结合measure Gaussian就可以得到一个new Gaussian, 如下图所示：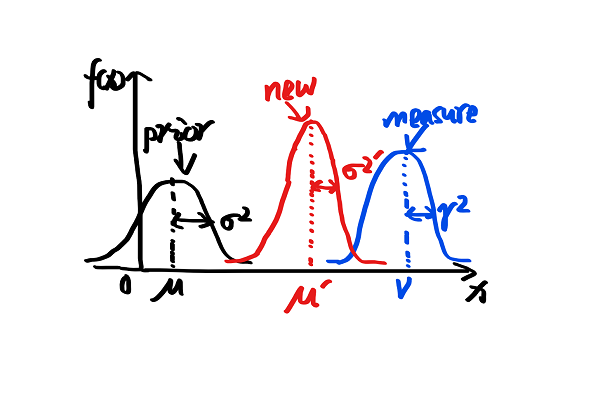
　
　　用数学公式描述如下：
$$ μ^{‘}= \frac{μr^2+vσ^2}{r^2+σ^2} $$

$$ σ^{2’}= \frac{1}{\frac{1}{r^2}+\frac{1}{σ^2}} $$

Predict Gaussian

　　在prior Gaussian的基础上，我们可以得到一个motion Gaussian，如下图所示：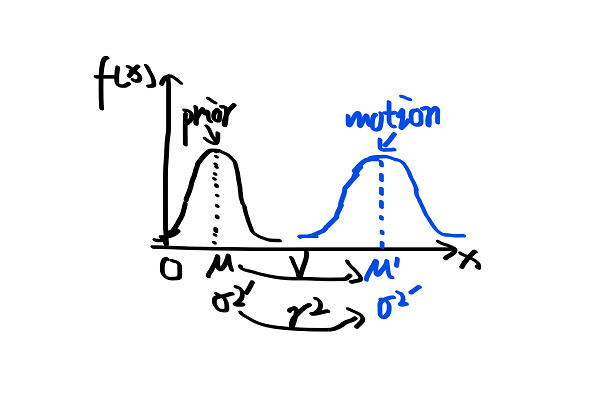

　　用数学公式描述如下：
$$ μ^{‘}= μ + v $$

$$ σ^{2’}= σ^2 + r^2 $$

卡尔曼滤波

　　卡尔曼滤波是一个动态更新的循环过程，包括测量和预测两个部分，我们可以通过线性代数来描述卡尔曼滤波的计算过程（包括一维和二维），如下：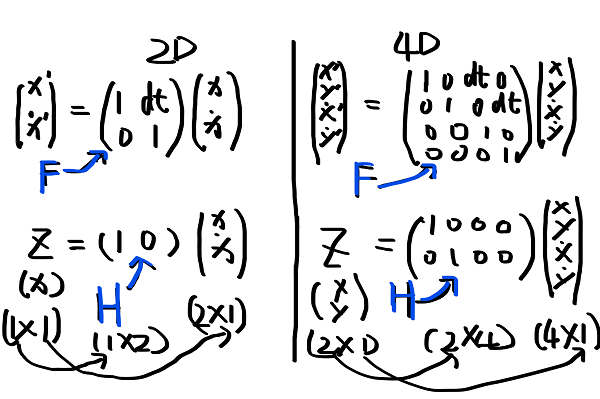

　　其中，F表示状态转换矩阵，H表示测量函数。

测量部分

$$ x^{‘}= Fx + u $$

$$ P^{‘}= F•P•F^T $$

预测部分

$$ y = Z - H•x $$

$$ S = H•P•H^T + R $$

$$ K = P•H•S^{-1} $$

$$ x^{‘}= x + (K•y) $$

$$ P^{‘}= (I - K•H)•P $$
　　其中， x表示状态的估计值，u表示运动矢量，P是用于表示不确定性的协方差矩阵，Z表示测量值， R表示测量，I表示单位矩阵。举个例子来说明这些矩阵应该如何取值：

# 2-D
measurements = [1, 2, 3]
x = matrix([[0.], [0.]]) # initial state(location and velocity)
P = matrix([[1000., 0.], [0., 1000.]]) # initial uncertainty
u = matrix([[0.], [0.]]) # external motion
F = matrix([[1., 1.], [0, 1.]]) # next state function
H = matrix([[1., 0.]]) # measurement function
R = matrix([[1.]]) # measurement uncertainty
I = matrix([[1., 0.], [0., 1.]]) # identity matrix

# 4-D
measurements = [[1., 17.], [1., 15.], [1., 13.], [1., 11.]]
initial_xy = [1., 19.]
dt = 0.1
x = matrix([[initial_xy[0]], [initial_xy[1]], [0.], [0.]]) # initial state (location and velocity)
u = matrix([[0.], [0.], [0.], [0.]]) # external motion
# initial uncertainty: 0 for positions x and y, 1000 for the two velocities
P =  matrix([[0., 0., 0., 0.], 
             [0., 0., 0., 0.], 
             [0., 0., 1000., 0.], 
             [0., 0., 0., 1000.]]) 
# next state function: generalize the 2d version to 4d
F =  matrix([[1., 0., dt, 0], 
             [0., 1., 0., dt], 
             [0., 0., 1., 0.], 
             [0., 0., 0., 1.]]) 
# measurement function: reflect the fact that we observe x and y but not the two velocities
H =  matrix([[1., 0., 0., 0.], 
             [0., 1., 0., 0.]]) 
# measurement uncertainty: use 2x2 matrix with 0.1 as main diagonal
R =  matrix([[0.1, 0.], 
             [0., 0.1]])
I =  matrix([[1., 0., 0., 0], 
             [0., 1., 0., 0.], 
             [0., 0., 1., 0.], 
             [0., 0., 0., 1.]]) # 4d identity matrix

　　卡尔曼滤波常用于传感器的数据融合和物体追踪之类的问题，而且由于计算量不大，被广泛应用于工程领域。